Learned one-shot imaging
Learned supershot/sim-source pair for one-shot imaging.
Learn sources and super shot simultaneously, reproducible at OneShotImaging.jl
\[ \newcommand{\pluseq}{\mathrel{+}=} \]
Objectives and scope
Seismic imaging’s main limiting factor is the scale of the involved dataset and the number of independent wave-equation solves required to migrate thousands of shots. To tackle this dimensionality curse, we introduce a learned framework that extends the conventional computationally reductive linear source superposition (e.g., via random simultaneous-source encoding) to a nonlinear learned source superposition and its corresponding learned supershot. With this method, we can image the subsurface at the cost of a one-shot migration by learning the most informative superposition of shots.
Method
Simultaneous-source imaging takes advantage of the linearity of the wave equation by combining encoded (e.g., via random weights or time shifts) shot records together, reducing the number of wave-equation solves and therefore the cost of imaging. Because of the linearity, the same linear transformation can be applied to the sources to maintain source-shot consistency. To further reduce imaging costs, we propose using nonlinear encodings, and to compensate for the inability to apply the corresponding transform to the source, we simultaneously learn the nonlinear source and nonlinear data encodings with two deep networks. The first network takes shot records as input and outputs a learned supershot. The second network produces the associated nonlinearly encoded simultaneous source given this supershot. Lastly, we migrate the supershot using the nonlinear simultaneous source to obtain the one-shot seismic image. To jointly train these networks, we propose supervised and unsupervised formulations. In the supervised method, networks aim to minimize the difference between the predicted image and the ground-truth seismic image. Our unsupervised approach eliminates the need for true models, making the technique applicable in practice, by minimizing the difference between the observed data and the migrated-demigrated supershots. Additionally, since the training only relies on supershot migration, the total cost of training is lesser than the conventional migration of all single shots.
Results
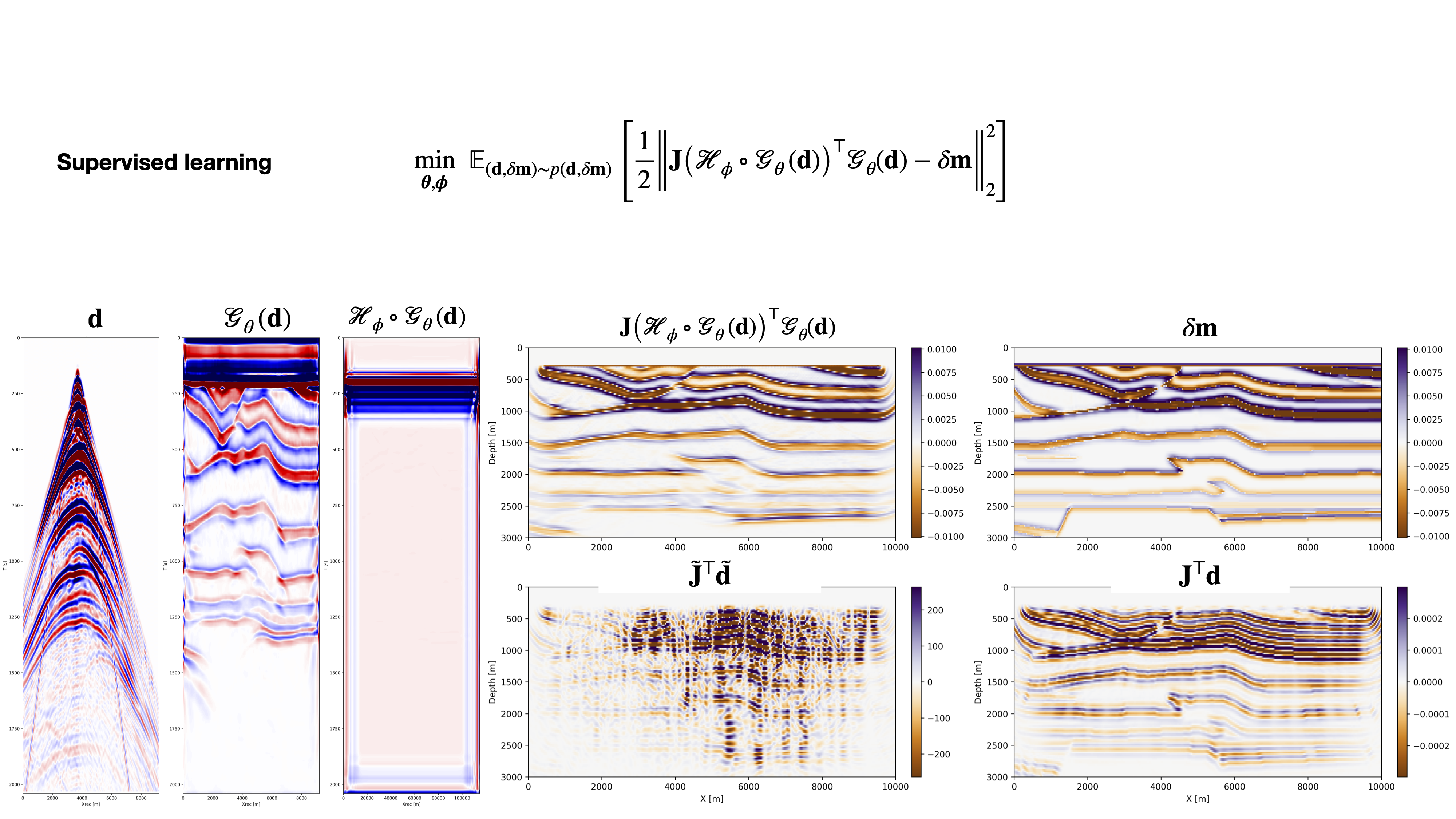
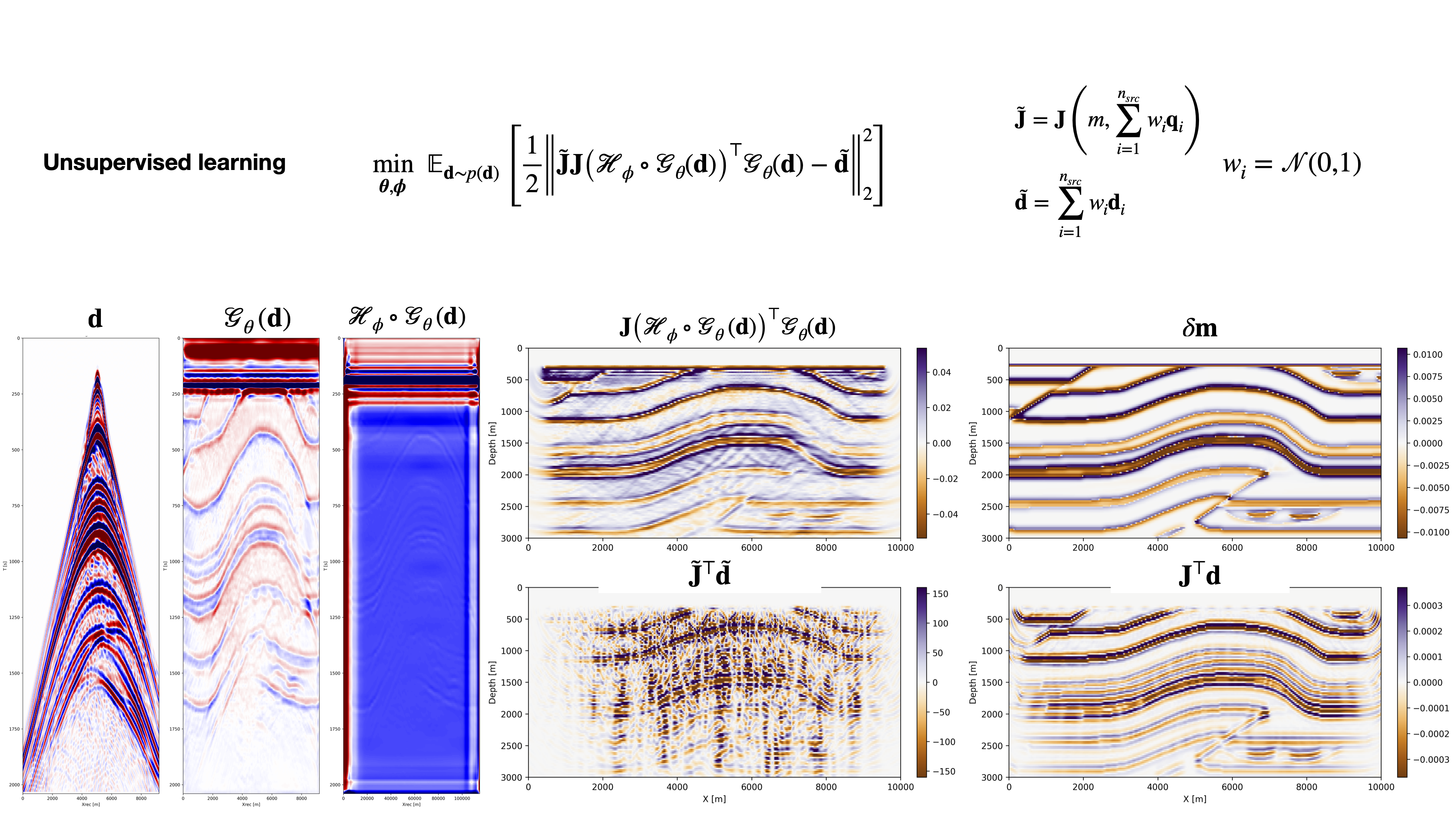
We apply the proposed one-shot imaging approach to a previously unseen shot data and slice. The cost of one-shot imaging is approximately the same as a single shot migration as network evaluation costs are negligible. Results for the learned supervised and unsupervised one-shot imaging are presented in Figures 1 and 2, respectively. For reference, the original shot data are included on the left, followed by the learned supershot data and learned source. Corresponding images are plotted on the right. Figure 1 shows that the learned one-shot reverse-time migration (RTM) result constitutes a major improvement compared to the image obtained with conventional random source encoding (juxtapose images in the first column on the left). The one-shot imaging result is also better than conventional sequential source RTM since it is closer to the true reflectivity plotted at the top of the right column. This improvement in the image’s frequency content can be explained by the fact that in the supervised learning formulation the networks are jointly trained to produce broadband seismic images. Similarly, we find that similar observations are true for the unsupervised case, except that the improvement in image quality is slightly less pronounced. Besides being computationally inexpensive and providing high-fidelity images since the source encoding is learned from data, our method requires no knowledge of the source signatures and learns to extract information from the data on the image.
Significance
We introduced the first instance of learned nonlinear simultaneous-source encoding, enabling one-shot seismic imaging. After incurring initial training costs, the method is capable of producing high-fidelity images at the cost of migrating a single shot record, which entails a drastic reduction in migration costs. We introduced supervised and unsupervised training formulations, the latter of which only relies on a dataset of shot records from several seismic surveys, making it applicable in realistic settings. Additional material is available at https://slimgroup.github.io/IMAGE2023/.
Supplementary material
Introduction
(Deans 2002) -Summary statistics reduce the size of incoming datasets while maintainting the same posterior distribution p(x|y) = p(x|summary) (Radev et al. 2020) -Summary networks learn to reduce the size of incoming datasets and maximize informativeness of the summarized data due to joint learning of summary network and posterior learning network. -hand waves an argument that jointly trained networks will maximize the mutual information between h(y) and x (Müller et al. 2021) -Goes in to further detail and rigoursly proves that jointly trained networks will maximize the mutual information between h(y) and x (Bloem-Reddy and Teh 2020) suggests to use learned layers that are invariant under a certain transformation. This transformation is described by the probabilistic assumption on your data.
Methodology
Here we present our formulation for a learned simultaneous source-data pair for seismic imaging. We propose two training formulations, one that relies on knowledge of the true perturbation (supervised), and the other that solely relies on the observed data (unsupervised). Fundamentally, we are introducing a formulation that learns a single supershot and corresponding source that maximally informs seismic imaging. Next section describes the design of the deep networks that enable this goal.
Summary networks
To handle the high-dimensionality of seismic data and, we use summary networks (Radev et al. 2020) that are designed to exploit the intrinsic low-dimensional structure [ref needed to curvelet etc] of seismic data. These deep networks compress the observed seismic data \(\mathbf{d}\) while maximally preserving the information useful for inferring the unknown seismic image \(\delta \mathbf{m}\). A major aspect of the architectural design of a summary networks are exploiting the invariances in data, e.g., invariance to permutation (Bloem-Reddy and Teh 2020). This is achieved by choosing neural architectures with functional forms that explicitly respect the intrinsic invariances in data. For example in the case of seismic imaging, the order of shot records has no effect on the final seismic image. To make this invariance explicit in the design of our network, we sum the shot records and feed it to a deep convolutional neural network.
Supervised
The simplest formulation aims to learn the supershot and simultaneous source that best inform the model perturbation, given the surface recorded data. Mathematically, it means that we are trying to fit the true model perturbation with two networks that learn a single supershot and simultaneous source for the Jacobian from the individual field recorded shot records. Mathematically, the learning can be written as: \[ \min_{\boldsymbol{\theta}, \boldsymbol{\phi}} \ \mathbb{E}_{(\mathbf{d}, \delta \mathbf{m}) \sim p(\mathbf{d}, \delta \mathbf{m})} \left[ \frac{1}{2} \Big\| \mathbf{J}\big(\mathcal{H}_{\phi} \circ \mathcal{G}_{\theta} \left(\mathbf{d}\right)\big)^\top \mathcal{G}_{\theta}(\mathbf{d}) - \delta \mathbf{m} \Big\|_2^2 \right], \tag{1}\]
where \(\mathcal{G}_{\theta}\) is the summary network that maps shot records to a learned, nonlinearly mixed supershot at the receiver locations, \(\mathcal{H}_{\phi}\) is the neural network responsible for estimating the associated nonlinearly encoded simultaneous source, and \(\circ\) is the composition operator. The objective function matches the predicted seismic image, obtained by migrating the supershot \(\mathcal{G}_{\theta}(\mathbf{d})\) via the adjoint Born imaging operator, \(\mathbf{J}\), to the ground truth seismic image \(\delta \mathbf{m}\). We note that to evaluate the gradient of the objective function with jointly respect to \(\boldsymbol{\theta}\) and \(\boldsymbol{\phi}\), the gradient of the Jacobian with respect to its input (nonlinearly encoded source) is required. This derivative is, however, trivial to obtain with JUDI.jl thanks to its high-level linear algebra abstraction and integration with automatic differentiation framework in Julia.
Unsupervised
To extend our approach to more realistic settings, we propose an unsupervised learning one-shot imaging approach that only requires a dataset of seismic shot records from several surveys. We formulate the problem as a minimization of the following objective function:
\[ \min_{\boldsymbol{\theta}, \boldsymbol{\phi}} \ \mathbb{E}_{\mathbf{d} \sim p(\mathbf{d})} \left[ \frac{1}{2} \Big\| \tilde{\mathbf{J}} \mathbf{J}\big(\mathcal{H}_{\phi} \circ \mathcal{G}_{\theta}(\mathbf{d})\big)^\top \mathcal{G}_{\theta}(\mathbf{d}) - \tilde{\mathbf{d}} \Big\|_2^2 \right ], \tag{2}\]
where \(\tilde{\mathbf{d}} = \sum_{i=1}^{n_{\text{src}}} w_i \mathbf{d}_{i}\) is a random super shot with \(w_i := \mathcal{N}(0, 1)\) and \(\tilde{\mathbf{J}}\) is the corresponding simultaneous source born modeling operator. While this formulation ivolves an additional demigration (and therfore and additional migration to compute hte gradient), we do not require any knowledge of the true model perturbation but only the data. We could therefore in theory use this formulation for a wide range of datasets at once to generalize to any survey.
Synthetic case studies
We illustrate our method on a realstic 2D imaging problem. We created a dataset of 2000 2D slices by extracting slices out of the 3D overthrust model. We then split this dataset into 1600 slices for trainng and 400 slices for testing. For each 2D slice, we generate 21 shot records. One of the main advantage of our one-shot imaging method is that we only require a single migration-demigration per iteration. Therefore, we can perform 21 epochs before arriving to a computationnal cost equivalent to the plain standard RTM imaging of each slice. Since we only perform 15 epochs, our method is overall cheapper than computing the RTM on every single shot if we include the cost of training.
We trained the networks, both in the supervised and unsupervised case, for 15 epochs with a learning rate of \(.0004\) using the Adam optimizer.
Discussion and conclusions
We introduced data-domain learning method that provides high accuracy imagies of the subsurface through one-shot imaging. We trained a network that learns the simultenous source and supershot that most inform the subsurface from the field recorded data. We showed that we obtain high accuracy images of the subsurface that contain broader frequency range than standard imaging and does not require prior knowledge of the source. Additionnally, the overall computationnal cost of training does not exceed the traditionnal cost of imaging.
References
Acknowledgement
This research was carried out with the support of Georgia Research Alliance and partners of the ML4Seismic Center.
Software availability
Results presented here can be reproduced with the software and examples in OneShotImaging.jl distributed under MIT license.