A Digital Twin for Geological Carbon Storage with Controlled Injectivity
Abstract
We present an uncertainty-aware Digital Twin (DT) for geologic carbon storage (GCS), capable of handling multimodal time-lapse data and controlling CO2 injectivity to mitigate reservoir fracturing risks. In GCS, DT represents virtual replicas of subsurface systems that incorporate real-time data and advanced generative Artificial Intelligence (genAI) techniques, including neural posterior density estimation via simulation-based inference and sequential Bayesian inference. These methods enable the effective monitoring and control of CO2 storage projects, addressing challenges such as subsurface complexity, operational optimization, and risk mitigation. By integrating diverse monitoring data, e.g., geophysical well observations and imaged seismic, DT can bridge the gaps between seemingly distinct fields like geophysics and reservoir engineering. In addition, the recent advancements in genAI also facilitate DT with principled uncertainty quantification. Through recursive training and inference, DT utilizes simulated current state samples, e.g., CO2 saturation, paired with corresponding geophysical field observations to train its neural networks and enable posterior sampling upon receiving new field data. However, it lacks decision-making and control capabilities, which is necessary for full DT functionality. This study aims to demonstrate how DT can inform decision-making processes to prevent risks such as cap rock fracturing during CO2 storage operations.
Introduction
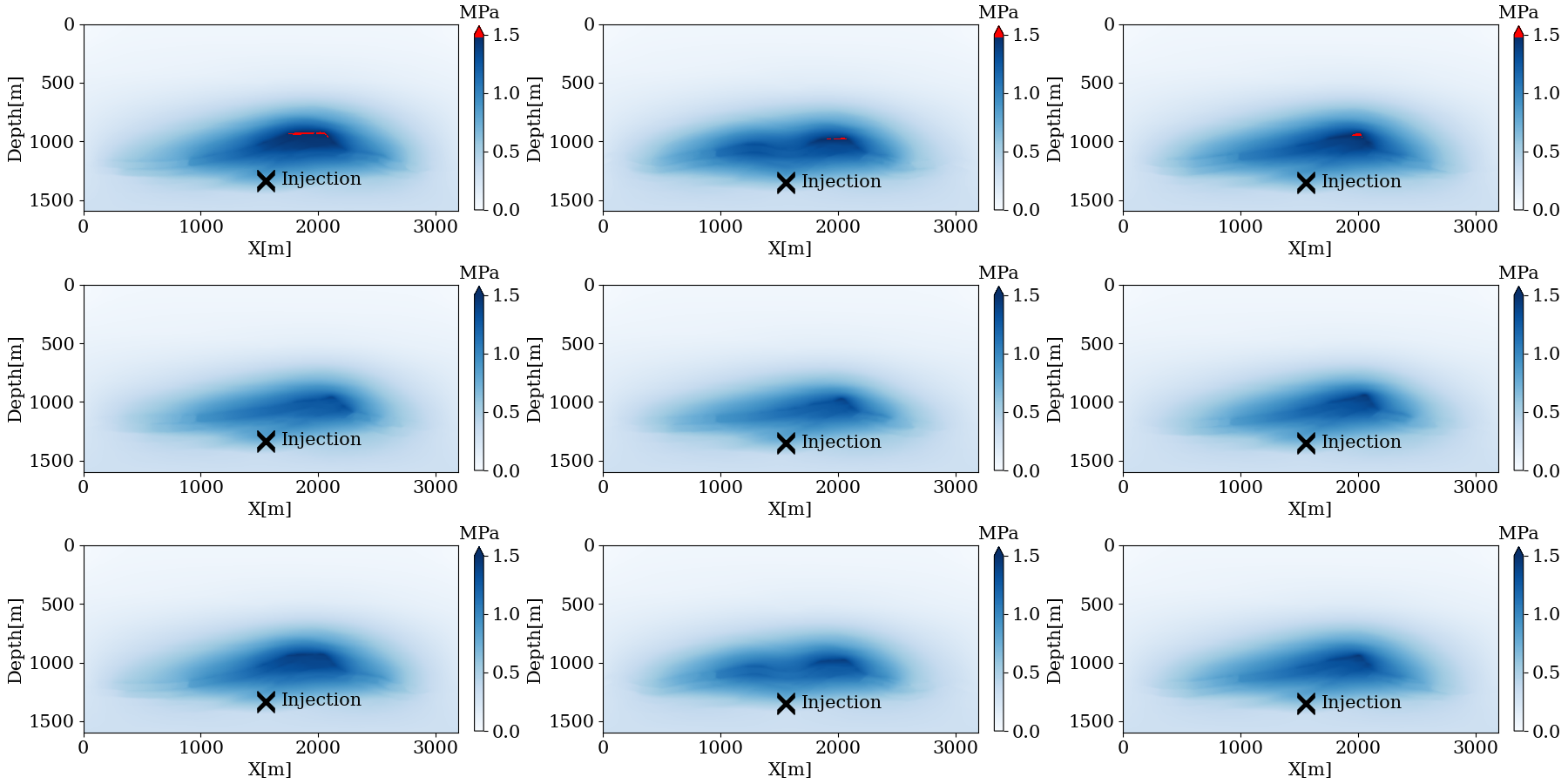
Digital Twins refer to dynamic virtual replicas of subsurface systems, integrating real-time data and employing advanced generative Artificial Intelligence (genAI) methodologies, such as neural posterior density estimation via simulation-based inference (Cranmer, Brehmer, and Louppe 2020) and sequential Bayesian inference (Papamakarios, Sterratt, and Murray 2019; Kruse et al. 2021). Thanks to combination of these advanced Bayesian inference techniques, our approach is capable of addressing challenges of monitoring and controlling CO2 storage projects. These challenges include dealing with the subsurface’s complexity and heterogeneity (seismic and fluid-flow properties), operations optimization, and risk mitigation, e.g. via injection rate control. Because our Digital Twin is capable of handling diverse monitoring data, consisting of time-lapse seismic and data collected at (monitoring) wells, it entails a technology that serves as a platform to integrate seemingly disparate and siloed fields, e.g. geophysics and reservoir engineering. In addition, recent breakthroughs in genAI, allow Digital Twins to capture uncertainty in a principled way (Yu et al. 2023; Herrmann 2023; Gahlot et al. 2023). By employing training and inference recursively, the Digital Twin trains its neural networks on samples of the simulated current state—i.e., the CO2 saturation/pressure, paired with simulated imaged seismic and/or data collected at (monitoring) wells. These training pairs of the simulated state and simulated observations are obtained by sampling the posterior distribution, \(\mathbf{x}_{k-1}\sim p(\mathbf{x}_{k-1}\vert \mathbf{y}^\mathrm{o}_{1:k-1})\), at the previous timestep, \(k-1\), conditioned on field data, \(\mathbf{y}^\mathrm{o}_{1:k-1}\), collected over all previous timesteps, \(1:k-1\), followed by advancing the state to the current timestep, followed by simulating (seismic/well) observations associated with that state. Given these simulated state-observation pairs, the Digital Twin’s networks are trained, so they are current and ready to produce samples of the posterior when the new field data comes in—i.e. \(\mathbf{x}_{k}\sim p(\mathbf{x}_{k}\vert \mathbf{y}^\mathrm{o}_{1:k})\). While this new neural approach to data assimilation for CO2 storage projects provides what is called an uncertainty-informed Digital Shadow, it lacks decision making and control, which would make it a Digital Twin (Thelen et al. 2022), capable of optimizing storage operations while mitigating risks including the risk of fracturing the cap rock by exceeding the fracture pressure. The latter risk is illustrated in Figure 1, where the first row contains simulated samples of the pressure difference at timestep \(k=4\), between the reservoir pressure and hydraulic pressure, without control. These samples for the simulated state exceed the fracture pressure and are denoted by the red areas. This manuscript will demonstrate how the Digital Twin can make informed decisions to avoid exceeding the fracture pressure.
Methodology
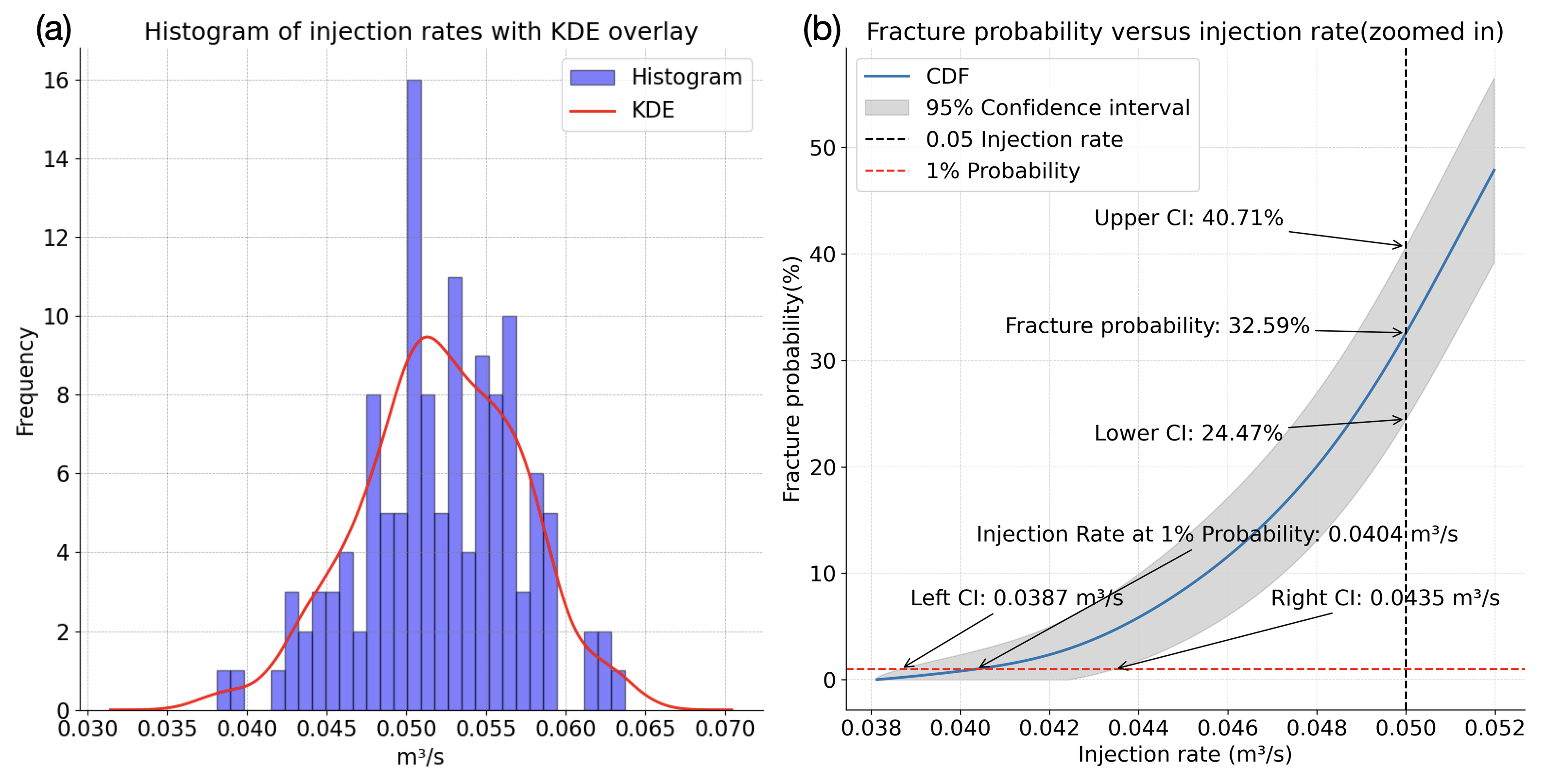
To make uncertainty informed decisions on adapting the injection rate, 128 samples of the state (see second row Figure 1), \(\{\mathbf{x}^{(m)}_{3}\}_{m=1}^{128}\), and permeability, \(\{K^{(m)}\}_{m=1}^{128}\), are drawn at time-step \(k=3\) from the posterior distribution, \(\mathbf{x}_{3}\sim p(\mathbf{x}_{3}\vert \mathbf{y}^\mathrm{o}_{1:3})\), for the state conditioned on the observed time-lapse data, and from the distribution for the permeability, \(K\sim p(K)\). To find the optimized injection rate, we first calculate for each sample, \(K\) and \(\mathbf{x}^{(m)}_{3}\), the optimized injectivity by \(\max_{q_3} q_3\Delta t \ \ \text{subject to} \ \ \mathbf{x}_{4}['p']<\mathbf{p}_{\max}\) where \(\mathbf{p}_{\max}\) is the depth-dependent fracture pressure, and \(\mathbf{x}_{4}=\mathcal{M}_3(\mathbf{x}_{3}, \mathbf{K}; q_3)\) the state’s time-advancement denoted by the symbol \(\mathcal{M}_3\). For the fluid-flow simulations, the open-source Julia package JUDI.jl and JutulDarcy.jl are used. Results of these optimizations are included in Figure 2(a), which contains a histogram of the empirical fracture frequency as a function of injection rates at time \(k=3\). Given this histogram, our task is to maximize the injection rate given a pre-defined confidence interval (e.g. 95 %), so that the fracture probability remains below a certain percentage e.g. 1%. With these simulations, and the fact that fracture/no-fracture occurrences are distributed according to the Bernoulli distribution, we will demonstrate that we are able to select an injection rate that limits fracture occurrence to the prescribed probability with a prescribed confidence interval. For instance, we can compute \(Pr([\mathbf{x}_4['p']>p_{\max}]<0.01)<1-0.025\), which corresponds to selecting an injection rate that leads to fracture rate of \(<1\%\) with \(97.5\%\) confidence. The confidence interval is halved, because only conservative (left) injection rates will be selected (see Figure 2(b)).
Results
To calculate injection rates that mitigate the risk of exceeding the fracture pressure, we proceed as follows. First, because the optimized injection rates are close to the fracture pressure, we consider these optimization as approximations to the injection rates where the fracture pressure are exceeded. Next, Kernel Density Estimation (KDE) is applied to produce the smooth red curve in Figure 2(a). This smoothed probability function is used to calculate the Cumulative Density Function (CDF), plotted in Figure 2(b). Using the fact that non-fracture/fracture occurrence entails a Bernoulli distribution, confidence intervals can be calculated, \(\pm Z_{\frac{\alpha}{2}} \sqrt{\frac{\hat{p}(1 - \hat{p})}{128}}\) where \(\hat{p}\) represents the CDF (blue line) and \(Z_{\frac{\alpha}{2}}=1.96\) with \(\alpha=0.05\). From the CDF and confidence intervals (denoted by the grey areas), the following conclusions can be drawn: First, if the initial injection rate of \(q_3 = 0.0500 m^3/s\) is kept, the fracture probability lies between 24.47 – 40.71% (vertical dashed line) and has a maximum likelihood of 32.59%, which are all way too high. Second, if we want to limit the fracture occurrence rate to 1% (red dashed line), then we need to lower the injection rate to \(q_3=0.0387\mathrm{m^3/s}\). To ensure the low fracture occurrence rate of 1%, the reduced injection rate is chosen as the smallest injection rate within the confidence interval. As can be observed from Figure 1 (third row) and Figure 2(b), lowering the injection rate avoids exceeding the fracture pressure at the expense of injecting less CO2. Out of 128 samples, 43 samples are fractured with the initial injection rate, while only one sample is fractured with the controlled injection rate.
Conclusion and discussion
We illustrate how Digital Twins can be used to mitigate risks associated with CO2 storage projects. Specifically, we used the Digital Twin’s capability to produce samples of its state (pressure), conditioned on observed seismic and/or well data. Using these samples, in conjunction with samples from the permeability distribution, we were able to capture statistics on the fracture occurrence frequency as a function of the injection rate. Given these statistics, we set a fracture frequency and choose the corresponding injection rate as a function of the confidence interval. By following this procedure, exceeding the fracture pressure was avoided by lowering the injection rate. The decision to lower the injection rate, and by which amount, was informed by the Digital Twin, which uses seismic and/or well data to capture reservoir’s state including its uncertainty.