Velocity Continuation for Common Image Gathers with Fourier Neural Operators
\[ \newcommand{\pluseq}{\mathrel{+}=} \]
Introduction
Common-image gathers (CIGs) are pivotal in migration-velocity analysis (MVA). However, MVA is often hindered by the computational burden of traditional migration methods. To bypass these limitations, we introduce a neural-surrogate learning approach that utilizes Fourier Neural Operators (FNOs, Li et al. 2020) to accelerate MVA. Following the velocity-continuation scheme of Siahkoohi, Louboutin, and Herrmann (2022), we train a survey-specific FNO to map the CIGs associated with one migration-velocity model to another without remigration. This methodology leverages the capacity of FNOs to approximate complex PDE-based mappings, rendering computational cost at inference negligible, thereby expediting MVA. By enabling rapid generation and evaluation of CIGs across various velocity models, it offers a pathway to quickly examine velocity models according to preferred properties and to quantify uncertainties in imaged reflectivities at the same time. Additionally, this methodology paves the way for inverse design optimization, updating velocity models to produce CIGs with desirable characteristics.
Methodology
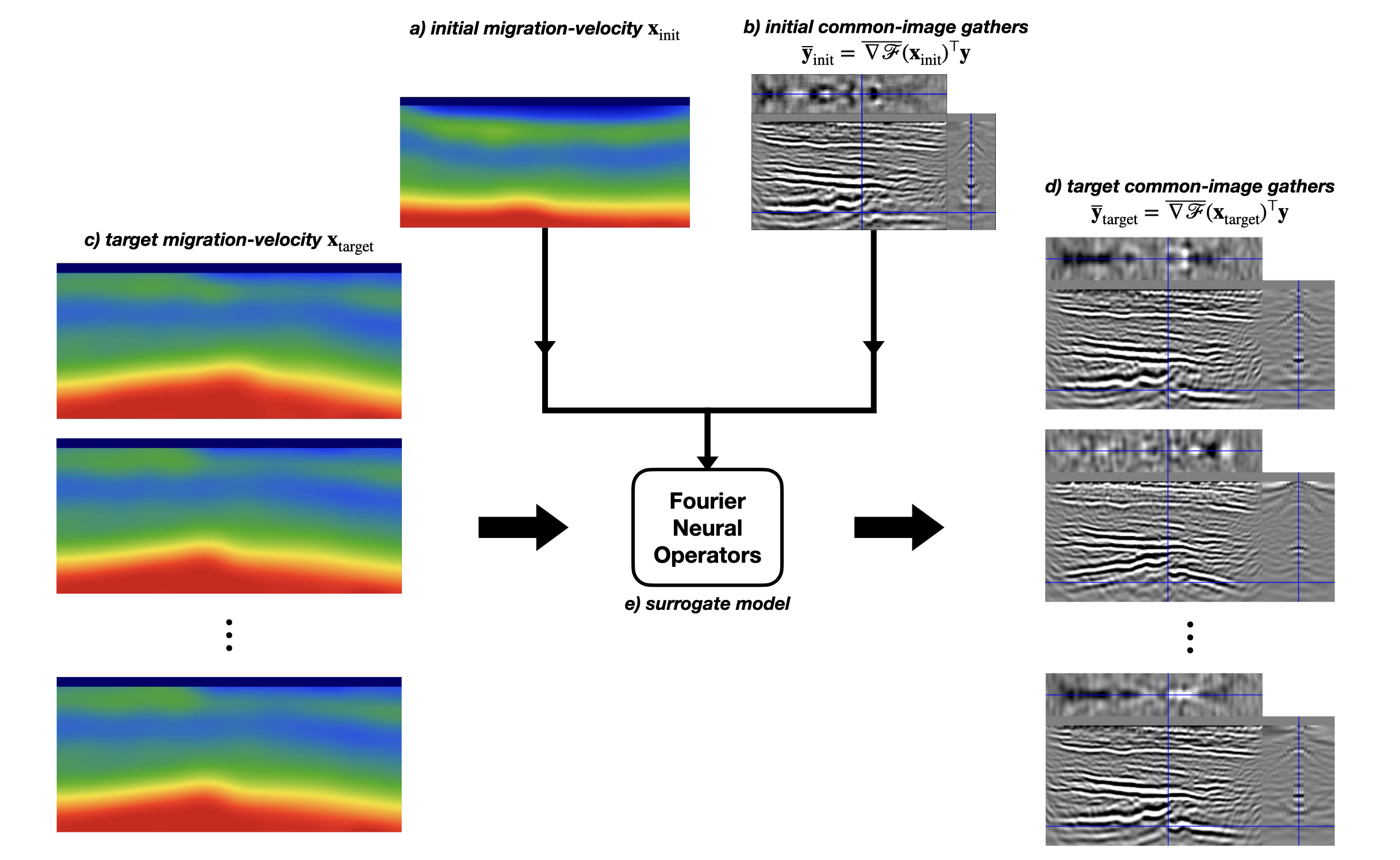
We conduct a case study on a 2D slice of the Compass model. We generate observed data with 256 sources and 32 ocean bottom nodes, using a Ricker wavelet with central frequency of 0.015 Hz. We assume absorbing boundaries in our study. We add uncorrelated band-limited noise with an SNR of 12 dB for realism. For a given migration-velocity model, CIGs are computed. To train the network to generate CIGs for new migration-velocity models without remigration, 500 new migration-velocity models (Figure 1 (b)) are generated and used to generate CIGs to form our training dataset (Figure 1 (c)). Given these models and CIGs, a FNO is to trained to map \(a)\) initial migration-velocity model, \(b)\) its CIG, and \(c)\) target migration-velocity models, to the CIGs associated with the target migration-velocity models (Figure 1 (d)).
Results
Figure 2 displays the FNO prediction in the subsurface-offset domain across various velocity models in an unseen test dataset. Despite some minor errors, the FNO prediction successfully captures the focusing pattern of the CIGs, and correctly produces the imaged reflectivities at the near zero-offsets. Computationally, the upfront training cost could potentially be reduced by transfer learning techniques. At inference, our trained FNO achieves \(3200\times\) speed-up compared to numerical computation of CIGs. These findings substantiate the computational efficiency of the FNOs in generating CIGs for many velocity models, underscoring its applicability in real-time migration-velocity analysis. This framework also presents a way to select good posterior samples of velocity models so that they exhibit desirable properties in their CIGs, making it a good choice of a postprocessor for velocity models produced by generative artificial intelligence workflows (Yin et al. 2023). Additionally, it enables fast uncertainty quantification of imaged reflectivities with respect to many velocity models. In addition to this, the framework could also be pivotal in performing inverse design optimization. By updating our background velocity models such that they yield CIGs with specific, desirable properties, we can further refine our understanding of seismic data. This work is made reproducible at FNO-CIG using distributed Fourier Neural Operators implemented in ParametricOperators.jl.
Acknowledgement
This research was carried out with the support of Georgia Research Alliance and partners of the ML4Seismic Center.