Enhancing Full-Waveform Variational Inference through Stochastic Resampling and Data Augmentation
Introduction
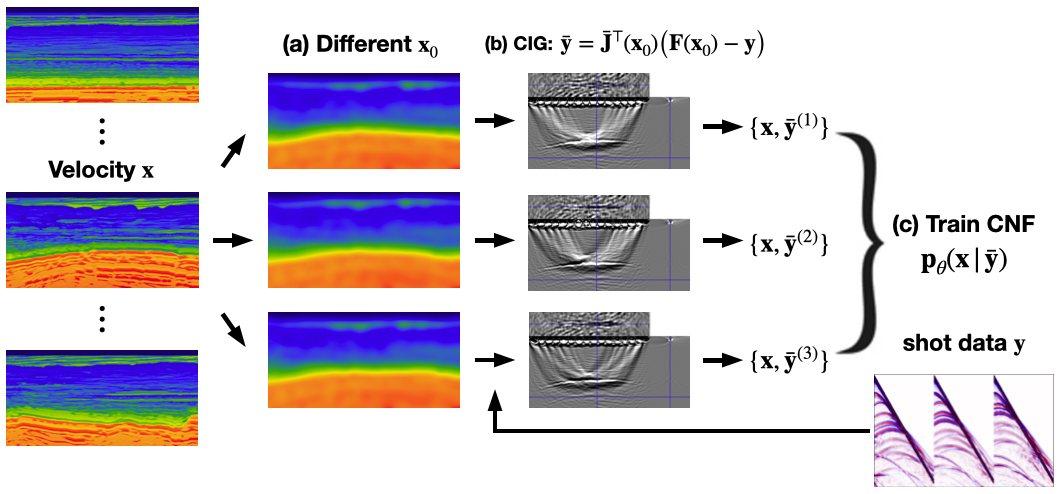
Full-Waveform Inversion (FWI) corresponds to a computationally expensive iterative optimization scheme that determines migration-velocity models by minimizing the discrepancy between observed seismic shot data and data generated by a forward model parameterized by the velocity. Recent advancements, such as full-Waveform variational Inference via Subsurface Extensions (WISE, Yin et al. (2023)) in simulation-based inference (Cranmer, Brehmer, and Louppe 2020), produce amortized neural posterior estimates that enable fast online inference of the velocity. These neural approximations to the posterior distribution, \(p_{\boldsymbol{\theta}}(\mathbf{x}\vert\mathbf{y})\approx p(\mathbf{x}\vert\mathbf{y})\) with \(\mathbf{x}\), the velocity model, \(\mathbf{y}\), the shot data, and \(\boldsymbol{\theta}\), the network weights, are obtained with variational inference, which requires extensive off-line training. Aside from providing statistically robust estimates via the conditional mean, \(\mathbb{E}_{\mathbf{x}\sim p_{\boldsymbol{\theta}}(\mathbf{x}\vert\mathbf{y})}(\mathbf{x})\), these neural posterior also provide a useful metric of the uncertainty in terms of the variance \(\mathbb{V}_{\mathbf{x}\sim p_{\boldsymbol{\theta}}(\mathbf{x}\vert\mathbf{y})}(\mathbf{x})\). To make this amortized inference approach computationally feasible, we follow Yin et al. (2023) and train on pairs \(\left\{(\mathbf{x}^{(m)}, \mathbf{\bar{y}}^{(m)})\right\}_{m=1}^M\), where the \(\mathbf{\bar{y}}^{(m)}\) stand for subsurface-offset Common Image Gathers, computed from each shot dataset, \(\mathbf{y}^{(m)}\). While CIG’s as physics-based summary statistics are better suited to inform the posterior than plain migration—i.e, they preserve information even when the migration-velocity model is poor, their performance still depends on the choice of the initial migration-velocity model, \(\mathbf{x}_0\). During this talk, we will study the impact of varying initial background-velocity models on the quality of the amortized neural posterior sampler. We will also investigate how augmenting the training set with different initial background-velocity models can lead to improved performance.
Methodology
By interpreting the initial migration-velocity model as stochastic latent variables—i.e., \(\mathbf{x}_0\sim p(\mathbf{x}_0\vert \mathbf{x})\) with \(\mathbf{x}\sim p(\mathbf{x})\), we propose to augment the training pairs, \(\left\{(\mathbf{x}^{(m)}, \mathbf{\bar{y}}^{(m)})\right\}_{m=1}^M\), with \(\mathbf{\bar{y}}^{(m)}\)’s computed for one single initial migration-velocity model, \(\mathbf{x}_0\), with \(\mathbf{\bar{y}}^{(m)}\), obtained with multiple different (randomly perturbed) initial migration-velocity models, \(\mathbf{x}_0\sim p(\mathbf{x}_0\vert \mathbf{x})\). The aim of this training dataset augmentation is to improve the robustness of WISE—i.e., make its neural posterior estimation less dependent on the choice for the initial migration-velocity model, \(\mathbf{x}_0\).
Results
To improve the neural posterior estimation’s robustness, multiple initial migration-velocity models, \(\mathbf{x}_0\), are obtained by randomly perturbing the ground-truth velocity model, \(\mathbf{x}\), followed by extensive smoothing. Since this deformation is stochastic, we can sample an “infinite” number of background models, \(\mathbf{x}_0\sim p(\mathbf{x}_0\vert \mathbf{x})\), to be used during training, although in practice we regenerate the background model a few times (\(3-5\)) (Figure 1(a)). Then, new \(\mathbf{\bar{y}}^{(i)}\) are generated based on each \(\mathbf{x}_0^{(i)}\) and \(\mathbf{y}\) (Figure 1(b)), and the resulting \(\{\mathbf{x}, \mathbf{\bar{y}}^{(i)}\}\) pairs form a training dataset for the Conditional Normalizing Flow (CNF) (Figure 1(c)).
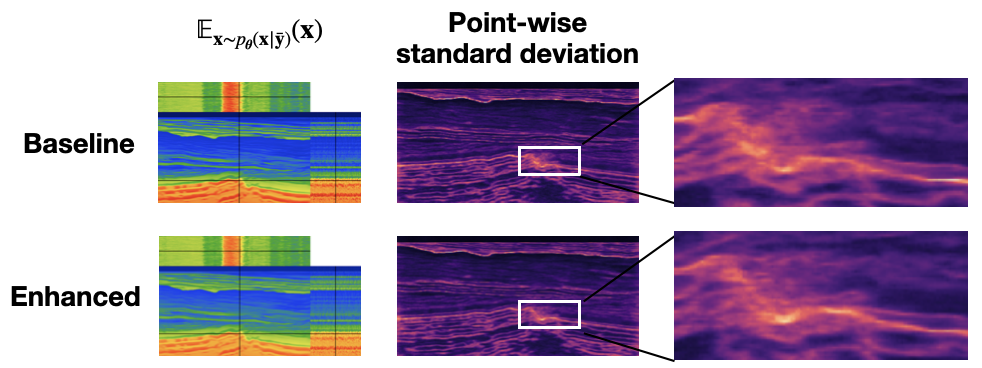
To evaluate our method, we divide the Compass model dataset (E. Jones et al. 2012) by allocating \(800\) pairs for training and \(150\) for testing. We train the baseline CNF on \(M=800\) velocity-extended image pairs, and train enhanced CNFs on augmented training pairs (\(M=1600, 2400, ...\) etc.). The trained CNFs are evaluated by structural similarity index measure (SSIM) and root mean square error (RMSE) of the posterior samples’ mean against the ground truth. SSIM improves from \(0.725\) to \(0.753\) while RMSE improves from \(0.110\) to \(0.107\) on \(150\) unseen test samples. Figure 2 shows the conditional mean and point-wise standard deviation of the baseline and the enhanced CNF posterior samples, where the enhanced CNF sampler aligns more closely with the ground truth. We observe the trend that the uncertainty is reduced as we increase the number of background-velocity model regenerations during training. This implies that the uncertainty information in the baseline has yet not captured the uncertainty fully due to the choice of a fixed background-velocity model while our method has learned to incorporate this uncertainty information into the final inference result.